こんにちは。デザイン芸人の「デザインや」です。
残さず数えることが好きです。
「3*3」を数える
今回は世間の喧騒をしばし忘れて
「3*3」
この世界に浸って数え上げることにします。
数えるのはもちろん、東京オリンピック・パラリンピックの公式エンブレムに関してです。
※以下「五輪エンブレム」と表記します。

この五輪エンブレムを、3*3の正方形に区切ります。
<イメージ>
┌-┬-┬-┐
|・|・|・|
|-+-+-|
|・|・|・|
|-+-+-|
|・|・|・|
└-┴-┴-┘
区切られた格子内の図形1個ずつを「デザイン要素」とみなし、ばらばらに置き直すとします。
さて、全部で何種類の置き方があるでしょうか?
その配置パターンを数えていきます。
謝辞
当記事におけるエンブレムの画像(描画データ)は、次のページから取得しました。ありがとうございます。
- 東京五輪2020エンブレムで学ぶSVG超入門|qiita.com(2015/08/09付)
- 【数学】東京オリンピックエンブレムの面積を求める|togetter.com(2015/07/30付)
結論:五輪エンブレム「3*3」組み合わせの数
現状の各パーツをそのまま使うとすると、組み合わせの数は、次のとおりです。
(1)色のない世界
- 向き固定:504通り(=9×8×7)
- 向き任意:4,032通り
(2)色付きの世界
- 向き固定:10,080通り(=(1)×20)
- 向き任意:161,280通り(=(1)×2×20)
(3)パラリンピックとの混合世界
「色なし」の場合
(1)と変化なし。
「色付き」の場合
9つのグリッド全体で、{オリンピック}{パラリンピック}どちらの要素を採用するかの組み合わせは、
2の9乗=512通り なので、
- 向き固定:5,160,960通り(=(2)×512)
- 向き任意:82,575,360通り(=(2)×512)
条件しだいでまだまだ増やせる
これらの組み合わせは、
- 配色パターンの拡張・応用のさせ方
- 構成要素のラインナップの自由度
しだいで、まだまだ増えます。
素敵です。
はじめに:定義
五輪エンブレムのロゴ部分は、3×3のグリッド(格子)に分けられます。
区切りの線を加えると、こんな感じです。

グリッド(場所)の番号
便宜上、左上から右へ順に番号を振っておきましょう。
<グリッド番号>
1・2・3
4・5・6
7・8・9
です。電話のプッシュボタンの並び方と同じです。

「1」~「9」は、この「場所」「位置」の番号です。
この場所に、個々のパーツが置かれる。そんなイメージです。
パーツ(要素)の名前
格子1個単位での「形」に名前を付けておきます。
※まだ「色」は考慮しません
図形のパターンは大別して3種類あります。
- 正方形(square)
- 円(circle)
- 弧(arc)
英単語の頭2文字を取って、正方形は「sq」、円は「ci」と書くことにします。


左:正方形「sq」 右:円「ci」
弧は全部で4パターンあります。
弧の4パターンを分ける基準は次のとおりです(どちらも同じことを言ってます)。
- 円弧で区切られた扇形がどの点に向いて凸か
- 仮想の「円」の一部とすると、2次元平面の第何象限にあるか
この基準で、1~4の番号を振ります。
具体的には、右上の頂点から反時計回りに1,2,3,4です。
五輪エンブレムの要素で言えば、

は、「a2」
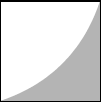
は、「a4」です。
配置パターンを数えたい
<配置パターンの例>
要するに、こういった図形の各要素をばらばらに置き直すパターンが、全部で何種類あるかを数えたいわけです。
数える1:五輪エンブレム要素の配置【無色版】
まずは、いつもそれを通して世界を見ている「色めがね」をいったん取り去って、色のない世界を考えます。
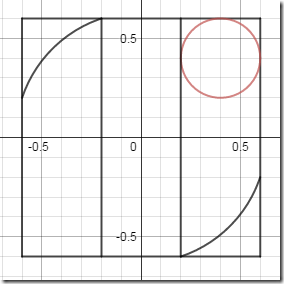
作成元:www.desmos.com/calculator/avpt8fugxw
ここで問題文を書き換えると、
- 「9つのグリッドに3種類のパーツを配置するパターンを数える」問題
となります。
たとえば五輪エンブレム(色なし版)は、次の模式図のように、
┌-┬-┬-┐
|a2|・|ci|
|-+-+-|
|・|・|・|
|-+-+-|
|・|・|a4|
└-┴-┴-┘
グリッド番号「1」「3」「9」にパーツが置かれている状態です。
(1)向き固定
パーツは3種類:「円ci」「弧a2」「弧a4」
ci、a2、a4の3つが置かれるグリッド位置(順不同)は
9*8*7= 504通り
(2)向き任意
弧の向きの区別がなくなるので、3つのパーツは2種類となる:
「円ci」と「弧ar」*2
ciの位置×(ar2枚の位置×それぞれの向き)は、
9C1 × { 8C2 × (4×4)}
= 9×{(8×7/2)×16)=9×28×16
= 4,032通り
※別解
「(1)向き固定」のパターンと比較すると、「a2」「a4」の区別がなくなる。
両者が入れ替わったパターンも同一となり、区別がなくなるから、配置の組み合わせは(1)の半分
504/2=252
その中で、「ar」2枚の向きのパターンが4×4通りとなるので
252×4×4=4,032通り
数える2:五輪エンブレム要素の配置【色つき版】
今度は色を付けます。
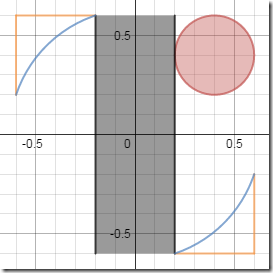
作成元:www.desmos.com/calculator/avpt8fugxw
中央縦1列に、黒い正方形(Square Black)「sb」が3枚加わった格好です。
問題文を書き換えると、
- 「9つのグリッドに6枚のパーツを配置するパターンを数える」問題
となります。
┌-┬-┬-┐
|a2|sb|ci|
|-+-+-|
|・|sb|・|
|-+-+-|
|・|sb|a4|
└-┴-┴-┘
たとえば五輪エンブレム(色つき版)のパーツ配置は、上の模式図のようになります。
これを言葉で表現すると、
- グリッド番号
- 「1」に弧2(金)
- 「3」に円(赤)
- 「9」に弧4(銀)
- 「2」「5」「8」に正方形(黒に近い濃灰)
のパーツが置かれている、という状態です。
これらの要素で、何通りの配置ができるかを数えます。
(1)向き固定
3つのパーツでの「色なしパターン」の組み合わせは「504通り」でした。
色がつくと、残りが「白地」だったところに、組み合わせとして《正方形「sb」を3つ配置するパターン》が加わります
残る6つのグリッドに、正方形「sb」を3つ配置するパターンは、6C3=20通りですから、
∴ 504 × 20 = 10,080通り
です。
(2)向き任意
色が付いているので、「弧」も色でパーツが区別されます。
向きとしては、
- 円ci(赤)は1通り(=回転しても変化なし)
- 弧a2(金)は4通り
- 弧a4(銀)も4通り
なので、この3つのパターンは
504(3枚配置:←9*8*7)×4(a2の向き)×4(a4の向き)
=8,064通り、
で(1)と同じく、残る6つのグリッドのうち、3つに正方形「sb」を配置するパターンは、6C3=20通りですから、
8,064 × 20 = 161,280通り
となります。
パラリンピックエンブレムの場合

比べると、「地の色」と「正方形」の色が反転して違っているだけです。
よって、「色なし」「色あり」とも五輪エンブレムとまったく同じです。
数える3:オリンピック・パラリンピックの混合パターン
くり返しますと、五輪・パラリンの両エンブレムの違いは、「地の色」と「正方形」の色彩が、白(#FFFFFF)黒(#373737)反転しているだけです。
色なしの場合
色彩を取り除くと五輪エンブレムと区別がありませんので、「数える1」で求めた
- 向き固定:504通り
- 向き任意:4,032通り
から変化なしです。
色付きの場合
どっちが表裏でもいいのですが、
ミックスパターンは「2の9乗」通り
グリッド1枚分のカードの表裏に「オリンピック要素」「パラリンピック要素」が描いてあるカードを想定してみます。
たとえば「正方形」パーツについて


表:黒正方形「sb」 このカードの 裏:白正方形「sw」
という具合です。
表裏をビット列表現してみる
ここで、表裏をビット列で表すことにして、
「五輪エンブレム」を
000
000
000
と表した場合、
「パラリンピックエンブレム」は、(地の色と正方形とを)反転させた
111
111
111
となります。
たとえば、下の表裏の状態をビット列で表現するならば
000
000
001
です。
こういう具合に、順に「表裏」を展開させてゆくと、「エンブレム」パターンだけでも、9つのグリッド全体で{オリンピック}{パラリンピック}どちらの要素を採用するかの組み合わせは、
9桁のビット列=2の9乗=512通り
存在します。
要素個々のグリッド配置パターンごとに、表裏の組み合わせが加わるので、組み合わせの数は(2)の結果を512倍して、
- 向き固定:5,160,960通り(= 10,080 × 512)
- 向き任意:82,575,360通り(= 161,280 × 512)
となります。
まとめ:素敵な「数理的バリアフリー」
既存のデザイン要素の「手持ちのカード」だけでも、最大で8000万通り以上の配置パターンを作れることがわかりました。
この五輪エンブレムの世界では、概念上「オリンピック」「パラリンピック」の要素が相互に交換可能であり、両者がまったく対等となっています。
数理上とはいえ、完全バリアフリーです。
そこが素敵です。
おわり


コメント